Dwars-stabiliteit in verband met hoogte zwaartepunt

[Peter Den]

Hoewel strikt genomen dit niet helemaal tot de aerodynamica behoord wil ik mijn visie toch graag op het theorieforum ter discussie geven.
Ik wil namelijk de veel gehoorde opvatting: een hoogdekker is stabieler dan een laagdekker nog eens toetsen.
Ik denk namelijk dat dit op foute aannamen berust.
Mocht ik na ampel discussie ongelijk blijken te hebben beloof ik me een maand stil te houden op het forum!

Mijn uitgangspunten zijn de volgende regels uit de eenvoudige mechanica:
a) Krachtenvectoren en koppels (momenten) kunnen in hun richting verplaatst worden.
b) Om de krachten en bewegingen van een lichaam (vliegtuig) te beschrijven dienen ze in hun relatie tot het zwaartepunt (centrum van massa) bepaald te worden.
c) Op een vleugel werkt een liftkracht die loodrecht staat op de projectie van de vleugel (in dit verband in frontaanzicht).
L= liftkracht van de vleugel
Lv= is de resultante-liftkracht in vertikale richting.
G= gewicht/zwaartekracht
Gr=resultaatgewicht is combinatie van centrifugaal kracht en gewicht.
Cv=middelpuntvliedende kracht
Cz=middelpuntzoekende kracht
Z=zijwaartse kracht op het zwaartepunt, slipkracht
a=arm

Links staat in de voorbeelden steeds de hoogdekker en rechts de laagdekker.
Waar het echter op neerkomt is dat, omdat alle krachten relateren aan het zwaartepunt, er in feite geen verschil is tussen een hoogdekker en een laagdekker.

1: Uitgangspositie, eenvoudige rechte vlucht met de krachten zoals meestal voorgesteld; L en G zijn aan elkaar gelijk, resultante=0
1a: correcte weergave: de krachten L en G grijpen aan in het zwaartepunt.

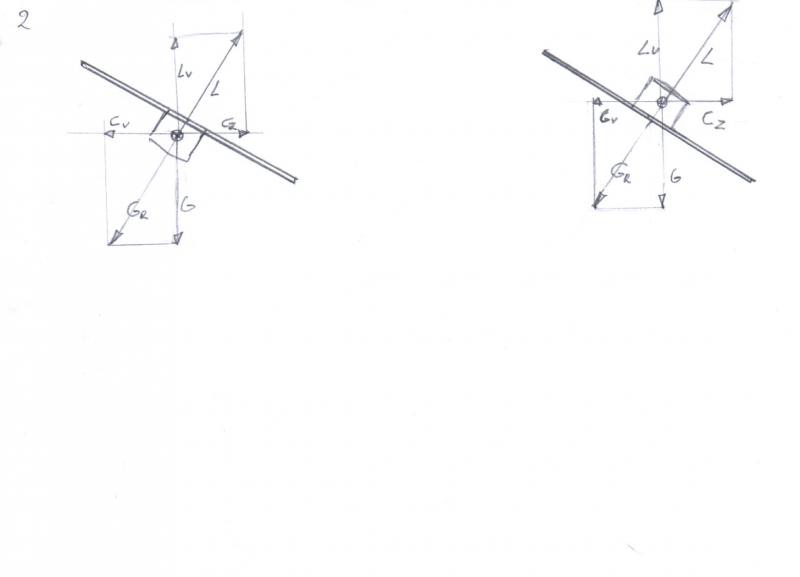
2: Bocht in krachtevenwicht: krachten Lv en G, L en Gr, Cv en Cz zijn met elkaar in evenwicht, geen momenten/koppels.

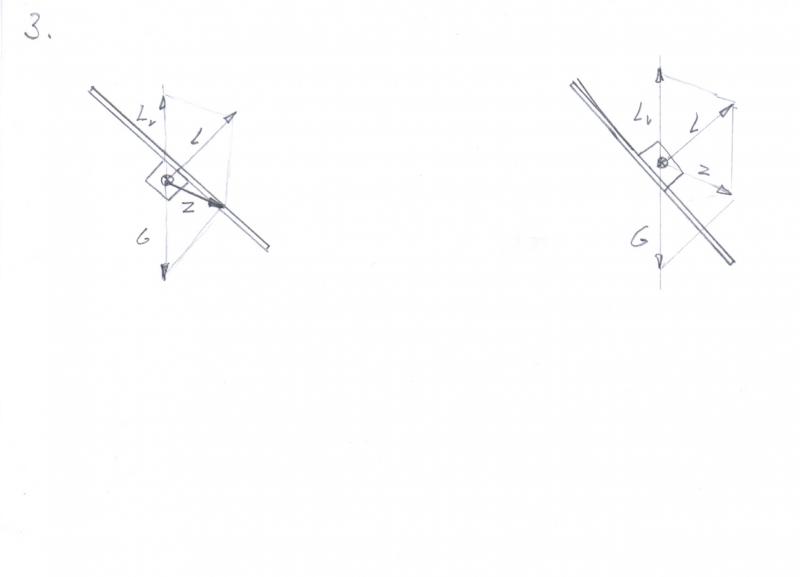
3: Hellend vliegtuig, geen bochtinput meer; afhankelijk van de snelheid zijn Lv en G wel of niet met elkaar in evenwicht, maar er ontstaat een slipkracht Z; het vliegtuig slipt naar binnen.

4a: vervolgfase: door de slip in kombinatie met V-stelling (of door zijdelinkse verschuiving van het aerodynamisch centrum van de vleugel, indien behoefte kom ik hier later op terug)
Ontstaat op de vleugel een asymmetrische liftverdeling: de koppels a1*l1 en a2*l2
4b: De resultante van deze asymmetrische liftverdeling is weer: L door het zwaartepunt en een restkoppel, namelijk a2*L2-L1.
Dit koppel draait het vliegtuig weer horizontaal en is het stabiliserende moment.

Er is echter geen verschil tussen een hoogdekker en een laagdekker in deze schema’s te vinden.

5: Nog ter illustratie van een veel voorkomend misverstand in verband met V-stelling: het is niet zo dat de lage vleugel bij voorbaat door zijn verticaal gerichte vector meer bijdraagt aan de lift dan de hooggelegen vleugel.
Namelijk beide vleugelhelften vormen een koppel a1*L1 en a2*L2
Hierdoor vallen a1 en a2 tegen elkaar weg in is de resultante zoals in
5b: met hier weer de enkele lift-resultante L die uiteraard weer door het zwaartepunt gaat.

Hopelijk is dit stof tot nadenken, maar zoals boer Koekoek placht te zeggen: ’mooi praten: bewijzen moeten we hebben’’
Hierbij een foto van een stel demo-modelletjes die ik getest heb.

Van links naar rechts een extreme laagdekker, een extreme hoogdekker en een neutrale schouderdekker.
Ik kan ieder aanbevelen deze proefjes zelf te doen: toegegeven, de extreme laagdekker ziet er in de lucht een beetje bizar uit, maar uit stabiliteitsoverwegingen is er vliegend geen verschil tussen deze 3 modellen.
Voor de volledigheid: de extreme laagdekker is ook gevlogen zonder V-stelling en de extreme hoogdekker heeft ook als laagdekker gevlogen door het stabilo andersom te buigen.

Heb ik het juist dan blijven vragen staan als: ’’waarom denken we dan dat hoogdekkers stabieler zijn dan laagdekkers?’’
Ik heb daar wel ideeën over, maar daar kom ik dan, indien daartoe uitgenodigd, wel op terug.
Hopend op constructief commentaar.
Peter.

 

[kuperus]

wat jij daar hebt getekend is een versimpeling van het geheel om uit te leggen hoe een bocht gevlogen wordt.

op onderstaande pagina wordt het lift-weight wat beter uitgelegd.

Aeronautics - The four forces of flight (LIFT AND WEIGHT) - Level 2

 

[Ariel]

negatieve v-stelling

Ik snap wel dat je voor deze voorbeelden het vliegtuig zwaartepunt ergens in het midden van de romp hebt geplaatst. Maar bedenk wel dat bij de meeste toestellen het werkelijke zwaartepunt op een andere plek ligt. Zo is het bijvoorbeeld bij de Saab 105 noodzakelijk dat de vleugels een negatieve v-stelling hebben anders zou het toestel te langzaam op de rolroeren reageren.
Wat ik me zeggen wil is dat elk ontwerp apart moet worden doorgerekend wil je vooraf weten hoe stabiel of instabiel het toestel zal vliegen.

Johannes

 

[Peter Den]

wat jij daar hebt getekend is een versimpeling van het geheel om uit te leggen hoe een bocht gevlogen wordt

Dat geld alleen voor tekening 2, daarna kom ik op helling zonder bocht.
Waarom het een versimpeling is, is mij niet duidelijk.
Met tekening twee wil ik aangeven dat er bij een correct gevlogen bocht geen verschil is tussen een hoog en een laagdekker.
De vraagstelling mijnerzijds is nog steeds: waarom wordt beweerd dat een hoogdekker in het algemeen rolstabieler is dan een laagdekker?
Ik herken dat niet in de krachtendiagrammen.
Wat ik in dit verband moet met de aanbevolen site is me niet duidelijk.

Ik snap wel dat je voor deze voorbeelden het vliegtuig zwaartepunt ergens in het midden van de romp hebt geplaatst

ik heb niet het zwaartepunt midden in de romp geplaatst, maar onder of boven de vleugel.
Met mijn tekeningetjes probeer ik aan te tonen dat dat niets uitmaakt. (ook hoger of lager niet)
Het geldt zowiezo niet voor mijn voorbeeld-modelletjes.
Als iemand denkt dat het niet klopt dient dat toch eens uitgelegd te worden.
Negatieve Vstelling is hier overigens niet het issue.

 

[serge pot]

jups ikheb een laagdekker jak3 ,accu hoog in de romp regelaar en servo'ssamen met ontvanger in de hartlijn van het vliegtuig .v-stelling is een 4graden per vleugel .vleugelvorm is elyptisch en spica profiel . alles duidt op een toestel wat eigenlijk instabiel zou moeten zijn . tegendeel is waar ., dankzij de v stelling is hij enorm stabiel en reageert zeer direct aan de knuppel mede dankzij een perfect zwaartepunt . het is eigenlijk een beginners toestel welke je kunt gebruiken om lekker te raggen , hij straft je niet af .
vleugelverdraaienig is ook een factor die mee speelt . het is niet alleen gewicht tov vleugel.

 

[Henri Zikken]

Laat ik je dan bij deze uitnodigen om uit te leggen waar dan het misverstand in jouw visie vandaan komt.. niet omdat ik denk dat je ongelijk hebt, maar omdat ik gewoon nieuwsgierig ben..

En los daarvan, respect dat je de moeite hebt genomen e.e.a. zo uit te werken!

 

[Psygho (Emil)]

Ik heb geen idee, heb er geen klaas van gegeten, maar +1 voor de mooie uitgebreide openingspost!

Ontopic: Ik blijf dit volgen, want interesant is het wel....

 

[Ariel]

Ik snap nu je vraagstelling, blijkbaar heb ik jouw verhaal niet goed gelezen.
Een hoogdekker is stabieler dan een laagdekker dat heb ik nog niet vaak iemand horen zeggen. Ook heb ik zelf al genoeg praktijkervaring met laag en hoogdekkers.

Johannes

 

[serge pot]

vroeger gold dat wel idd . een hoogdekker had toen vaak geen rolroeren en een laagdekker wel (daarom de kreet een hoogdekker is stabieler ) had niks met zwaartepunt en draagpunt te maken ,maar die toestellen werden zo gebouwd.

geef een hoogdekker minder v stelling en rolroeren en je hebt nagenoeg het zelfde effect als een laagdekker die met rolroeren standaard is uitgerust .

eigenlijk zou je het eens moeten proberen met een dubbeldekker 1 x vliegen zonder ondervleugel en 1x vliegen zonder boven vleugel(als de instel hoeken van zowel boven en ondervleugel gelijk zijn en mits de constructie dit aan kan )dan zou je het pas echt moeten merken

 

[Flying Davy]

Om even op het V-stelling verhaal te reageren. Volgens mij maak je hier een denk-/beredeneringsfout. De lage vleugel heeft namenlijk een Liftfactor die rechtstreeks omhoog gaat(90 graden verticaal op de vleugel), terwijl de hoge vleugel een Liftfactor heeft die ietwat gekanteld staat. Hierdoor is de verticale component van de lage vleugel groter dan de verticale component van de hoge vleugel. Deze verticale component tilt de lage vleugel op(immers er is een resultante kracht in de verticale componenten op de vleugels) en dus wil het toestel terugrollen naar een normale horizontaalvliegende positie.

Heb over het hoog en laagdekker verhaal ook nog even zitten denken en logischerwijs kom ik op het volgende(maar ben hier niet zeker van dus de experts mogen me corrigeren):
Doordat bij een hoogdekker het gewicht onder de Liftvector zit zal het CG ervoor zorgen de de massa zich weer recht onder de vleugel wil vestigen(als een bal aan een touwtje wat je uit het midden haalt en loslaat zeg maar). Hierbij zit het CG aan de buitenkant van de bocht en wil dus terug naar de binnenkant van de bocht, terug naar een horizontale situatie. Bij de laagdekker echter zit het CG dus boven de liftvector en zal dit ervoor zorgen dat de massa juist door wil zakken. Hierbij zit het CG aan de binnenkant van de bocht wat dus resulteerd in het doordraaien naar de bocht, onstabiel dus.
Klinkt misschien niet helemaal logisch door Jip en Janneke taal, maar probeer het voor iedereen duidelijk te maken zodat ook de niet aerodynamicus het kunnen snappen.

En dan nog even zonder een verklaring: Heel veel(eigenlijk alle die ik ken) 1:1 vliegers die zowel hoog- als laagdekker hebben gevlogen, geven aan dat de hoogdekkers vaak meer eigen stabiel zijn dan de laagdekkers.
Geen verklaring, maar wel een feit dat het zo ervaren word.

 

[Ariel]

In de praktijk is het allemaal veel complexer dan op deze voorbeeldplaatjes met de getekende krachten. Dit is puur theoretisch maar de getekende krachten kloppen inderdaad.
Voor mij houd het hierbij op, dit snap ik.
Maar ik wil graag meer weten over stabiliteit. Het heeft mijn interesse en ik heb vele vragen daarover.

Johannes

 

[XiM]

Je uitgangspunt b klopt niet. Je kan alleen de zwaartekracht modelleren als een kracht die aangrijpt in het zwaartepunt.
De liftkracht grijpt aan in het centrum van lift (liftpunt????). Ik heb geen idee wat de juiste term voor dit punt is, maar liftpunt voldoet voorlopig.

Juist het feit dat beide punten op een andere locatie zitten zorgt voor stabiliteit/instabiliteit. Figuur 1 is dan ook de juiste en niet figuur 1a.

Probeer voor de gein jouw redenatie eens toe te passen op een satéstokje dat je met de punt op op je vingertop probeert te balanceren. Als alle krachten in het zwaartepunt zouden aangrijpen zou dat ook niet instabiel zijn.

 

[kuperus]

in principe kloppen de tekeningen wel, maar alleen als je het gemiddelde van het hele vliegtuig pakt. dus alle krachten bij elkaar. echter vergeet je een ding in dit geheel het punt wat in het vliegtuig getekend staat is niet het CG maar een willekeurig in het midden van het vliegtuig gekozen punt.

de aangrijping van de exacte krachten is echter een heel ander verhaal.

en bij tekening 5a en b vergeet je tekening C waarbij beide lift krachten ontbonden worden per vleugel.
dan kun je pas zien wat het effect is omdat je dan een arm en kracht hebt en dus een moment. hieruit zul je zien dat het moment van de liggende vleugel veel groter is, dan het moment van de staande vleugel.

 

[DirkSchipper]

Er zit volgens mij (ik heb het niet uitgebreid doorgelezen) één cruciale fout in jouw tekeningen.

De liftkracht grijpt altijd ergens (midden) in de vleugel aan.
Maar de zwaartekracht zit bij een hoogdekker eronder, en bij een laagdekker erboven.
In jouw tekeningen grijpen lift en zwaartekracht beiden in hetzelfde punt aan.

Ergo,
- bij een hoogdekker zit het zwaartepunt onder het ophangpunt (liftoorsprong) en krijg je dus een hengende slinger, die altijd naar beneden wil hangen en dus auto-stabiel is.
- bij een laagdekker zit het zwaartepunt boven de liftoorsprong. Vergelijk het met een ballpoint die je op zijn punt op je vinger zet en dan rechtop probeert te balanceren. Dit is een instabiele situatie. Als je niets doet valt ie om ...

En nu wil ik je een maand niet meer horen! :rolling:



Dirk.

 

[Ariel]

Juist het feit dat beide punten op een andere locatie zitten zorgt voor stabiliteit/instabiliteit. Figuur 1 is dan ook de juiste en niet figuur 1a.

Precies, de onderlinge afstand van het zwaartepunt ten opzichte van het aerodynamisch centrum zijn beslissend hoe stabiel of instabiel een vliegtuig vliegt.
Voor mij is een mooi voorbeeld een glijscherm waarbij het zwaartepunt ver onder het aerodynamisch centrum ligt. Ik weet wel zeker als de piloot boven het scherm zou kunnen hangen dat deze combinatie instabiel zal vliegen.

Johannes

 

[Ad Bakker]

De liftkracht grijpt altijd ergens (midden) in de vleugel aan.

Toch heeft Peter gelijk met wat hij in zijn eerste post stelt "Krachtenvectoren en koppels (momenten) kunnen in hun richting verplaatst worden.". Voor evenwichtsbeschouwingen van een star lichaam kunnen kracht en momentvectoren verplaatst worden langs hun werklijn. Het werkelijke aangrijpingspunt daarvan op het lichaam doet er niet toe. Maar dat geldt alleen voor zuiver statisch evenwicht.

Vergelijk het met een ballpoint die je op zijn punt op je vinger zet en dan rechtop probeert te balanceren. Dit is een instabiele situatie. Als je niets doet valt ie om ...

Voor stabiel evenwicht is het van belang welk koppel er op het lichaam ontstaat als er een kleine afwijking ten opzichte van de stabiele toestand ontstaat. Bij een gewicht dat ergens aan hangt treedt er bij een kleine verdraaiing een koppel op dat tegengesteld is aan die verdraaiing. De situatie corrigeert zichzelf, en er is sprake van stabiel evenwicht. Bij een gewicht dat op een punt onder het zwaartepunt rust (bijvoorbeeld die balpen op z'n punt) ontstaat er bij een kleine verdraaiing een koppel dat net deze verdraaiing meegaat en deze dus versterkt: hij valt dus om. Dan is er dan sprake instabiel evenwicht.

Hoe dit verder doorwerkt op Peter's beschouwingen heb ik nog niet bekeken. Daar moet ik nog eens over nadenken........
Ik heb over iets dergelijks wel eens nagedacht over de plaatsing van de propeller van een moerasboot. Intuïtief zou ik denken dat die vooraan zou moeten staan omdat die dan aan de boot "sleept" (aangrijpingspunt voor het zwaartepunt), en me dat stabieler leek dan een "duwende" propeller achterop (aangrijpingspunt achter zwaartepunt). Maar in de praktijk blijkt dat toch niet zo.

 

[TC01]

Peter, jou beredenering klopt, maar ga nu eens je testmodellen verzwaren door extra gewicht op de romp te bevestigen, en kijk dan wat het resultaat wordt van de testen.

 

[Ariel]

Peter, jouw demomodelletjes heb ik goed bestudeerd.
Wat jij over het hoofd ziet is het grote vlak wat als afstandhouder voor de vleugels dient.
Het oppervlak daarvan is zelfs groter dan het kielvlak. Dit vlak samen met het kielvlak zorgen voor een moment tijdens het zijlings afglijden (niet gecoördineerde bocht).
En daarom vliegen de demomodelletjes stabiel.

Johannes

 

[Henri Zikken]

Doordat de krachten niet in hetzelfde punt aangrijpen, ontstaat er in de 'bochtsituaties' een koppel. Dat is nu weggelaten in het hele verhaal.

Bekijk de hoogdekker in het 1e figuur. Daar staan de krachten goed. Lifkracht grijpt aan in de vleugel, CG in de romp. Bekijk nu alle andere figuren, daar gebeurt dit niet.

Maak nu die andere figuren eens zo dat dat wel zo is. Dan zul je zien dat er een koppel ontstaan in rollende situaties.

Daarbij wat theo zegt, wat is de vleugelbelasting van die vliegtuigjes.

Als laatste heeft de extreme laagdekker een v-stelling. Waarom? Voor een goede test, zou alles gelijk moeten zijn.

 

[Ariel]

Als laatste heeft de extreme laagdekker een v-stelling. Waarom? Voor een goede test, zou alles gelijk moeten zijn.

Dit schrijft Peter:
Voor de volledigheid: de extreme laagdekker is ook gevlogen zonder V-stelling en de extreme hoogdekker heeft ook als laagdekker gevlogen door het stabilo andersom te buigen.

Johannes